I have been thinking a lot about artificial intelligence lately. The subject has interested me for some years now, but I have not yet committed to any substantial research. I have read a few chapters in a book I bought a couple years ago (978-0136042594), watched about a dozen MIT lectures on YouTube, and read some odd number of online articles, but introductory knowledge is all I really have. That said, in all my unknowing, I still know that artificial intelligence will eventually beat us at everything.
I am going to use this writing to flesh out some of my largely uninformed thoughts, opinions, and conceptualizations. I have far from an expert understanding of ANY of the MANY approaches that have been applied in the field thus far. At this point, I know nothing more than the basics of the fundamentals. Some of what I am about to say might be jibberish. You have been warned.
People hate trial-and-error. From an algorithmic perspective, it is the most inefficient way to solve a problem. It just takes us too long. On the other side, it works every time. There are no exceptions – no circumstances in which the guess-and-check approach fails. The variables do not need to be transformed and arranged in a certain way for the method to work. It is a simple model, but not a trivial one. The word trivial implies a sort of unimportance, but things can be simple and still very important. The two words are often mistakenly interchanged. Have you ever said or heard someone say that a solution was trivial? Well, they probably meant simple. People write-off things labeled as trivial much like math teachers like to write off guess-and-check. In a world where everything is relative, can anything even be unimportant? Was the weight of the straw that broke the back of the camel trivial? Everything great that we have done has been the result of trial-and-error: cars, airplanes, computers – everything. It is a valid if not the most valid approach to solving problems.
AI will eventually beat us at everything because we will keep trying and failing until it does. Our laziness knows no bounds; we love to conserve energy. We try to produce the most output for the least input. We demand value. We strive for quality, consistency, and speed in more or less that order. Getting something done sooner is always better than getting something done later, but only so long as both results are equal in all other measures.
Computers already beat us in all of that. They are far less complicated than people – simpler – but they are certainly not trivial. With enough time, they will no doubt supersede us in everything we do. Computers are fast enough that they do not need the same level of algorithmic efficiency humans often require to solve complicated problems with many possible solution paths in a timely fashion. They can generate-and-test the unknown faster than we can choose and apply the well known. Their long paths can beat our shortcuts.
To clarify, a complicated problem is one that can be potentially solved in a number of different ways. The complication manifests itself in our yearning to solve it the best way. Whether we want to take the most familiar path, generate the most good for the least bad, produce the finest quality with the lowliest ingredients, make the most money for the least expense, achieve a major change with a minute amount of effort, realize the greatest results in the least time, or we just want to do something different, choosing which path to take when modeling the means to an end is wherein the complication lies.
Our motivations, current knowledge, and ability to reason about likely future outcomes based on an understanding of previous outcomes seriously affects our path choice. Sometimes the choice is even too difficult to make, so one is made to do nothing at all. It appears to me we favor shorter and more familiar paths for time and consistency. The more we know or can reasonably assume, the fewer steps we need to take, the faster we can move on to something else, and the less effort we need to expend in analysis.
The thing is computers (and robots and machinery and everything else we have made to make our lives easier) at their worst still outperform people at their best in almost every measurement that matters. They are designed to, after all. The slowest computer solving a problem in the least efficient way (or even every least efficient way) is still often times capable of producing the highest quality, most consistent results faster and with less energy than the fastest humans using the single most efficient model of solution ever could.
Computers do not need to remember shortcuts to best us because they process data so much faster than we do – they can multiply 9 times a number without fingers or times tables in a fraction of the time that we can with. They can solve problems in the most time-consuming ways (adding 9 four times, 3 twelve times, or 2 eighteen times) as well as every other way they know how and still come to 36 before we have even finished considering which models of solution could be used. In an increasing number of cases, computers do not need algorithmic efficiency to be more efficient than humans.
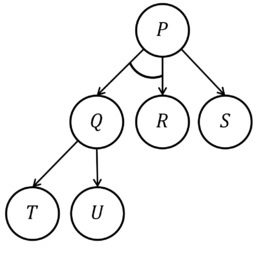
This is an “And-Or” tree. It is also called by different names in different professions. In cyber security, they are called “Attack” trees; in artificial intelligence, they are called “Goal” trees. They are used to represent a number of things, and I am going to give this one a triple purpose and use them interchangeably. For this example, goals can be interchanged with knowledge can be interchanged with state. The concept is the same for all three. We want to build on goals to achieve more goals. We want to use what we know to know more. We want to realize future states through the existence of past states. Every new step depends on the success of the previous step. The solutions are not the nodes, but the paths that help us achieve the goals, knowledge, or state that the nodes represent. In this image, Q was once a piece of knowledge that was obtained either by way of T, or by way of U. The current root node, P – our newest and most complicated state (complicated because there are many paths to choose from) can either be obtained by way of S, or by way of Q and R. Neither Q nor R is sufficient to obtain P on its own, but S is. Looking at this diagram, there are many ways in which we can reach P: we can simply depend on S, or we can know both Q and R. The existence of state Q, however, requires that we also reach the goal of either T or U.
Why explain the same concept using different words? Because different words in different contexts invoke different images and those different images each represent different paths to the same goal, piece of knowledge, or state – different methods of solution, different conclusions, different means to an end – much like there are many paths to a goal, there are many paths to knowledge and many paths to a particular state. The more paths you have to a goal, the more likely you are to find your way to it. Without a number of paths to our knowledge, we tend to lose track of both it and the reasoning used to establish it. Paths are also used to create new paths. Commonalities between points in a path suggest general importance while disparity between points suggests exceptional circumstances. More paths are better – to a point. All storage fills up eventually, or at least takes longer to index and compare.
Computers, on the other hand, can get by with far fewer paths. They don’t lose their way or forget. Their knowledge requires less overhead to maintain. Of course, they can store more paths, as well. While humans follow the paths they are most familiar with or assess a number of different known paths trying to find the one most applicable to a given problem, computers can often work their way through every path, compare every solution to every other, and produce a better analyzed answer than humans ever could. When we first narrow in on a path, decide through assumptions and brief analysis that the path is the shortest or most correct, and come to a solution accordingly – we fail to take into account a lot of information on other paths that might also be useful to us – especially if those paths are more involved (guess-and-check). When solving a new problem we never know for sure if the path we took was the best we could have taken, but we do not have time to try them all. A computer does. It can test through trial-and-error every path and make no such oversight. Further, computers can much more accurately assess dependencies.
Goals, knowledge, and state change with time, and at least with humans, paths expire when not reinforced. This is good for us as it keeps us in tune with what is relevant to us today (which is often what we think will be relevant to us tomorrow, based on what we know today). We are guess-and-checking the future based on the dependencies of our current knowledge, much like we set our future goals in consideration of past goals, or come by current states through the existence of past states. As alluded to earlier, even if we could store every single bit of knowledge and every single path that reinforces that knowledge, it would take longer to sort through than we have time for – and that’s a shame. We might have a better picture of what is true or false if we could analyze every step we took on the way to choosing solutions. Our shortcuts and ability to assume things allow us to start in the middle of trees, however, and eventually the leaves and branches get forgotten or at least overlooked as irrelevant details; but how is a leaf trivial to a root if everything is relative? One can argue that with no roots, there can be no leaves, but the same can be said in reverse: something has to capture the sunlight, after all. A root cannot support itself anymore than a leaf can. How do we ensure no path is overlooked or forgotten? How should paths be stored, indexed, and made available to future access for use in future problem solving?
Not unlike databases, there are pros and cons to consider… to normalize or not to normalize? That is the question. Normalized knowledge is undoubtedly the most efficient method of storage from a space conservation standpoint, but the retrieval of normalized data involves the retrieval of every dependency. In multi-variable problems, many dependencies exist, and path deduction becomes quite involved and time consuming. On the other hand, if state is stored in one and only one place, an update to it will effectually propagate across the entire tree, fostering an environment where everything is relative to everything else.
Unnormalized data lends itself to fewer dependencies, shorter paths, and faster lookups, but at the cost consistency. What works in one situation might not work in another if there is any difference at all in the two. Knowledge in one node might contradict knowledge in another, but with no relation between the two, how does one tell which path containing which node provides the better solution model to a given problem? If one path indicates that it is alright to lie, but another unrelated path demonstrates that is false, which one is more correct?
I’m not going to try and answer these questions because I feel I have made my point either way. It doesn’t really matter how (in) efficiently things are stored or accessed because regardless the method, artificial intelligence will eventually beat us at everything anyway.